You Know the Values for the Sine and Cosine of the Standard Angles. The Angle 67.5ã‚° Is Half of
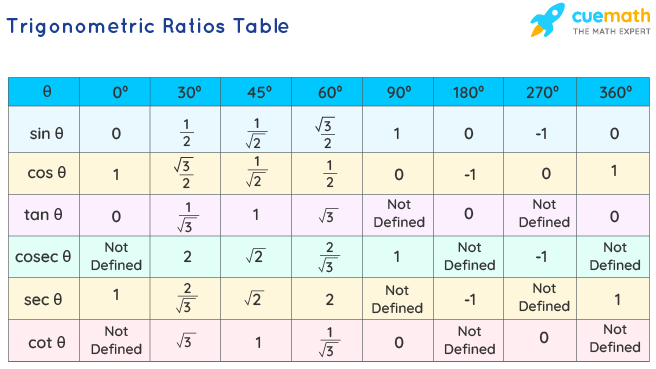
Trigonometric Table
The trigonometric table helps in finding the values of trigonometric ratios for standard angles such as 0°, thirty°, 45°, 60°, and 90°. Trigonometric tabular array comprises trigonometric ratios – sine, cosine, tangent, cosecant, secant, cotangent. These ratios, in short, are written as sin, cos, tan, cosec, sec, and cot. The values of trigonometric ratios of standard angles in a trig table are essential in solving trigonometry bug.
Trigonometry deals with the measurement of angles and problems related to angles. The term trigonometry is derived from a Latin word. Trigonometry makes utilise of the human relationship between the angles and sides of a triangle.
| 1. | What is Trigonometric Tabular array? |
| 2. | Trigonometric Values |
| 3. | Trigonometry Table for Standard Angles |
| 4. | How to Acquire Trigonometric Table? |
| 5. | Trigonometry Tabular array in Radians |
| 6. | FAQs on Trigonometric Tabular array |
What is Trigonometric Table?
The Trigonometric Tabular array is simply a collection of the values of trigonometric ratios for various standard angles including 0°, 30°, 45°, lx°, ninety°, sometimes with other angles similar 180°, 270°, and 360° included, in a tabular format. Considering of patterns existing inside trigonometric ratios and fifty-fifty between angles, it is easy to both predict the values of the trigonometry table and utilize the table as a reference to calculate trigonometric values for diverse other angles. The trigonometric functions are namely sine function, cosine part, tan function, cot function, sec function, and cosec function.
Trigonometric Values
Trigonometry deals with the human relationship betwixt the sides of a triangle (right-angled triangle) and its angles. The trigonometric value is a collective term for values of different ratios, such as sine, cosine, tangent, secant, cotangent, and cosecant in a trigonometric table. All the trigonometric ratios are related to the sides of a correct-angle triangle and their values are establish using the following ratios.
To recollect this easily remember the word "SOHCAHTOA"!
- SOH
Southine = Opposite / Hypotenuse
- CAH
Cosine = Adjacent / Hypotenuse
- TOA
Tangent = Opposite / Adjacent
Standard Angles in a Trigonometric Table
The values of trigonometric ratios for the angles 0°, 30°, 45°, 60°, and xc° in a trigonometry table are unremarkably used to solve the trigonometry bug. These values are associated with the measurement of the lengths and the angles of a correct-angle triangle. Thus, 0°, thirty°, 45°, 60°, and ninety° are chosen the standard angles in trigonometry.
Trigonometry Tabular array for Standard Angles
The trigonometric table is simply a collection of values of trigonometric functions of diverse standard angles including 0°, xxx°, 45°, 60°, 90°, along with with other angles like 180°, 270°, and 360° included, in a tabular format. Information technology is piece of cake to predict the values of the trig ratios in a trigonometric tabular array and to apply the table as a reference to calculate trigonometric values for various other angles, due to the patterns existing within trigonometric ratios and even between angles.
The table consists of trigonometric ratios – sine, cosine, tangent, cosecant, secant, and cotangent. In short, these ratios are written every bit sin, cos, tan, cosec, sec, and cot. It is best to remember the values of the trigonometric ratios of these standard angles.
Using the higher up table, values of sin π/half-dozen, cos π/six, tan π/half dozen, sin π/4, cos π/4, tan π/4, sin π/3, cos π/3, tan π/3, sin π/2, cos π/2, and tan π/2 in radians could be easily establish out. A trigonometric table has wide awarding in fields like science and engineering science.
A few key points that can be noted in the trigonometric tabular array are,
- The values for complementary angles present similar 30° and 60° in a trigonometric tabular array can exist computed using complementary formulas for the diverse trigonometric ratios.
- The value for some ratios in a trig tabular array is given as ∞ or "not defined". The reason for this is that while calculating the values, a "0" appears in their denominator, so the value becomes undefined and is said to be equivalent to infinity.
- There is a sign modify in the values in various places under 180°, 270°, etc for values of some trig ratios in a trigonometric table. This is due to the alter in the quadrant.
How to Learn Trigonometric Tabular array?
The trigonometric tabular array might seem complex at first, but it can be learned easily by only the values of sine for the eight standard angles. Before generating the table, there are few formulas that must exist followed as given beneath,
- tan x = sin x/cos x
- cosec x = ane/sin 10
- sec x = 1/cos x
- cot 10 = 1/tan x
Given below are the steps to create and retrieve a trigonometric table.
- Step 1: Create a table with the top row listing the angles such every bit 0°, 30°, 45°, 60°, 90°, and write all trigonometric functions in the showtime column such every bit sin, cos, tan, cosec, sec, cot.
- Stride 2: Determining the value of sin: Write the angles 0°, 30°, 45°, 60°, 90° in ascending guild and assign them values 0, 1, ii, 3, iv according to the order. Then, 0° ⟶ 0; 30° ⟶ 1; 45° ⟶ 2; 60° ⟶ 3; 90° ⟶ iv. Then divide the values by iv and square root the entire value. 0° ⟶ √0/ii; 30° ⟶ i /2; 45° ⟶ ane/ √2; sixty° ⟶ √3/2; ninety° ⟶ √(4/4). This gives the values of sine for these 5 angles. At present for the remaining iii use:
sin (180° − x) = sin x
sin (180° + 10) = -sin x
sin (360° − x) = -sin ten
This means,
sin (180° − 0º) = sin 0º
sin (180° + 90º) = -sin 90º
sin (360° − 0º) = -sin 0º
| Angles(in Degrees) | 0° | 30° | 45° | 60° | ninety° | 180° | 270° | 360° |
| sin | 0 | 1/2 | one/√2 | √3/2 | one | 0 | -1 | 0 |
- Step three: Determining the value of cos: sin (90° – x) = cos ten. Use this formula to compute values for cos x. For example, cos 45° = sin (ninety° – 45°) = sin 45°. Similarly, cos 30° = sin (xc° - 30°) = sin threescore°. Using this, you lot can easily find out the value of cos office as,
| Angles(in Degrees) | 0° | xxx° | 45° | threescore° | 90° | 180° | 270° | 360° |
| cos | one | √3/two | one/√2 | 1/2 | 0 | -1 | 0 | 1 |
- Step 4: Determining the value of tan: (tan x = sin 10/cos x). Hence, the value of tan function can be generated as,
| Angles(in Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| tan | 0 | ane/√iii | 1 | √3 | ∞ | 0 | ∞ | 0 |
- Step 5: Determining the value of cot: (cot 10 = one/tan x). Use the relation to generate the cot function as,
| Angles(in Degrees) | 0° | 30° | 45° | 60° | 90° | 180° | 270° | 360° |
| cot | ∞ | √three | 1 | 1/√3 | 0 | ∞ | 0 | ∞ |
- Stride six: Determining the value of cosec: (cosec 10 = one/sin x)
| Angles(in Degrees) | 0° | 30° | 45° | threescore° | ninety° | 180° | 270° | 360° |
| cosec | ∞ | 2 | √2 | 2/√3 | 1 | ∞ | -1 | ∞ |
- Pace 7: Determining the value of sec: (sec x = i/cos x)
| Angles(in Degrees) | 0° | 30° | 45° | threescore° | xc° | 180° | 270° | 360° |
| sec | one | 2/√iii | √2 | 2 | ∞ | -i | ∞ | i |
The following trigonometric table covers the value of trigonometric ratios for all basic angles ranging from 0º to 360º.
Trick to Remember Trigonometric Tabular array
Let us learn the one-hand trick for remembering the trigonometric tabular array easily! Designate each finger the standard angles as shown in the image. For filling the sine values in the trigonometry table, we will include counting of the fingers, while for the cos table we will but fill the values in reverse order.
- Step 1: For the sine table, count the fingers on the left side for the standard angle.
- Step 2: Divide the number of fingers by 4
- Footstep three: Take out the square root of the ratio.
Example 1: For sin 0°, there are no fingers on the left-hand side, therefore we will take 0. Dividing the zero past four nosotros get 0. Taking the square root of the ratio we would get the value of sin 0° = 0
Example 2: For sin 60°, there are iii fingers on the left-hand side. Dividing three past 4 we get (3/4). Taking the foursquare root of the ratio √(iii/4) nosotros would become the value of sin 60° = √3/2.
Similarly, we can detect out values for sin 30°, 45°, and 90° to make full the table.
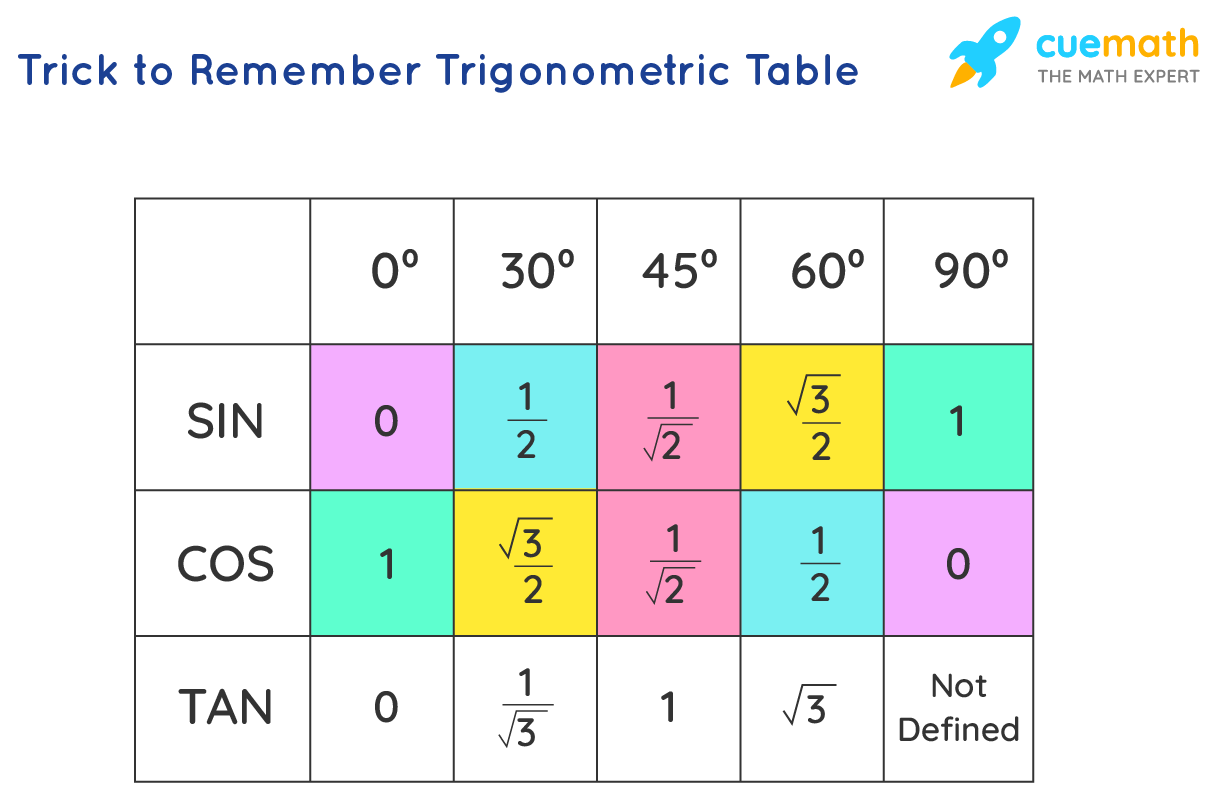
In gild to complete the cos tabular array, only fill in the values of sine in a reverse manner. For tan values, create the ratios by taking numerators of sine and cos values of the corresponding angle.
Given beneath is a list of trigonometric formulas that would aid you memorize the trigonometric table, based on the relationship betwixt different trigonometric ratios.
sin x = cos (ninety° – 10)
cos x = sin (xc° – ten)
tan x = cot (90° – x)
cot x = tan (90° – x)
sec x = cosec (90° – x)
cosec x = sec (xc° – x)
1/sin x = cosec x
1/cos x = sec x
one/tan x = cot 10
Trigonometry Tabular array in Radians
The trigonometric table for standard angles below presents the values of trigonometric ratios for the measure of angles given in radians.
☛ Related Topics:
- Trigonometry Formula
- Trigonometric Identities
- Trigonometric Ratios
Important Notes on Trigonometric Table
- Trigonometric values are based on the iii major trigonometric ratios: Sine, Cosine, and Tangent.
Sine or sin θ = Side opposite to θ / Hypotenuse
Cosines or cos θ = Adjacent side to θ / Hypotenuse
Tangent or tan θ = Side opposite to θ / Adjacent side to θ -
0°, 30°, 45°, sixty°, and 90° in a trigonometric tabular array are called the standard angles in trigonometry.
-
The angle values of trigonometric functions cotangent, secant, cosecant in a trigonometric table, tin can also exist calculated using these standard angles values of sine, cosecant, tangent.
-
All the higher angle values of trigonometric functions such every bit 120°, 390°, .... can be easily calculated from the standard angle values in a trigonometry table.
Examples using Trigonometric Table
-
Example ii: Can you determine the tiptop of the glacier given below using a trigonometric tabular array? Use of calculators is permitted.
Solution:The length of the hypotenuse is known to exist 20 units. We want to discover out the opposite side to the angle. Sine ratio uses the reverse side and hypotenuse. Remember the word "SOHCAHTOA"! SOH: Sine = Opposite / Hypotenuse. Thus, sin45º = Contrary/Hypotenuse, which gives 1/√2 = Opposite/20. Hence, Opposite = twenty/√two, Opposite ≈ xiv.fourteen. ∴ The height of the glacier is approx. 14.14 units.
Answer: Hence, the height of the glacier is approx. fourteen.fourteen units.
become to slidego to slidego to slide
FAQs on Trigonometric Table
What is the Trigonometric Table?
Trigonometric table or sin cos tabular array gives the values of trigonometric functions for the standard angles such as 0°, 30°, 45°, threescore°, and 90°, in a tabulated manner.
What are the Standard Angles in a Trigonometric Table?
The angles 0°, 30°, 45°, 60°, and ninety° in a trigonometric table are called standard angles, and the trigonometric values for these standard angles are commonly used to solve the trigonometry problems. These values are associated with the measurement of lengths and angles of the correct-angle triangle.
What Does the Infinity Value of the Trigonometric Ratio in the Trigonometry Tabular array Hateful?
Undefined values in a trigonometric table are oftentimes given an infinity (∞) value because the value is such large that at that place is no definite value to assign at this point.
What are Trigonometric Functions and their Types Used In Trig Table?
Trigonometric functions are defined as the functions of an angle of a right-angled triangle. In that location are 6 basic types of trigonometric functions or ratios used in the trigonometric table,
- Sin part
- Cos office
- Tan role
- Cot function
- Cosec office
- Sec function
How to Find the Value of Trigonometric Functions Given in Trigonometric Tabular array?
All the trigonometric functions in a trigonometric table are related to the ratios of sides of the triangle and their values can be easily institute by using the following relations:
- sinθ = Opposite/Hypotenuse
- cosθ = Adjacent/Hypotenuse
- tanθ = Opposite/Adjacent
- cotθ = ane/tanθ = Adjacent/Opposite
- cosecθ = ane/sinθ = Hypotenuse/Opposite
- secθ = 1/cosθ = Hypotenuse/Adjacent
What are the Six Basic Trigonometric Functions in Trigonometric Tabular array?
The six basic trigonometric functions in the trigonometric tabular array are Sine, Cosine, Tangent, Secant, Cotangent, and Cosecant office.
How Does a Trigonometric Table Work?
The trigonometric ratios table helps u.s.a. to observe the values of trig ratios for standard angles such as 0°, xxx°, 45°, lx°, and 90°. It comprises trigonometric ratios of sine, cosine, tangent, cosecant, secant, cotangent. These ratios are written in short as sin, cos, tan, cosec, sec, and cot.
Who Invented Trigonometry Table?
The Greek astronomer Hipparchus (127 BC) is believed to exist the commencement to brand a tabular array of trigonometric functions (based on the chords in a circumvolve).
What is the Easiest Mode to Acquire Trigonometric Tables?
To learn the one-paw trick for remembering the trigonometric table easily, designate each finger the standard angles. For filling the sine table we will include counting of the fingers. For the cos table, we will simply fill the values in reverse guild.
- Step 1: To find the values of sine functions in a trigonometric table, count the fingers on the left side for the standard angle.
- Step two: Split this number of fingers by 4.
- Footstep 3: Take out the square root of the ratio to find the final sine value.
For example, For sin 0°, there are no fingers on the left-hand side, therefore we will take 0. Dividing the zilch by 4 we get 0. Taking the square root of the ratio we would get the value of sin 0° = 0
Similarly, nosotros tin find out values for the sine ratio of other angles to fill up the table. For tan, split up the value obtained for sin function by the value obtained for cos role.
What is the Use of a Trigonometry Table?
A trigonometric tabular array is used to find the value of whatsoever trigonometric ratio for a given angle. The bones values of trig ratios for standard angles given in a trigonometry table tin exist used in the calculation of trigonometric ratios of other angles. These values find application in fields like applied science, architecture, etc.
Source: https://www.cuemath.com/trigonometry/trigonometric-table/
0 Response to "You Know the Values for the Sine and Cosine of the Standard Angles. The Angle 67.5ã‚° Is Half of"
Post a Comment